K-Map representation

Digital Teaching AidKarnaugh Mapping - Lesson 4Lesson Plan(introduction...)IntroductionKarnaugh mapTruth table to Karnaugh mapPairs, Quads, and OctetsOverlapping and Rolling

Pairs, Quads, and Octets

Pairs

Fig. 4-4: Four variable simplification

As you see in Fig. 4-4, only one variable goes from uncomplement to complement. Whenever this happens, you can eliminate the variable that changes form.

Proof:

X = A B C

Ex:

Fig. 4-5: Pairs

Whenever you see a pair first encircle it and then simplify to get the simplified Boolean expression:

Quad

Fig. 4-6: Quad

Quad: A group of 4 one's that are horizontally or vertically adjacent. End to end or in form of a square.

A quad eliminates two variables and their complements.

Proof:

(two pairs)

X = A B (C + C)

X = A B

Encircle the quad and step through the different one's in the quad and determine which two variables go from complement to uncomplement (or vs), these are the variables that drop out.

Ex:

Fig. 4-7: Quad

The variables B and D can be eliminated. So we get the following equation:

X = A C

Octet

Fig. 4-8: Octet

An octet eliminates three variables and their complements.

Proof:

(two quads)

X = A (C + C)

X = A

Karnaugh Simplifications

Process:

1. Draw the Karnaugh map
2. Look for octets and encircle them.
3. Look for quads and encircle them.
4. Look for pairs and encircle them.
5. Simplify and write down the equation.

Ex:

Fig. 4-9: Karnaugh map

Overlapping and Rolling

Overlapping groups

Ex:

Fig. 4-10: Karnaugh map

Groups can overlap to get a simpler equation:

Rolling the map

Ex:

Fig. 4-11: Karnaugh map

Instead of encircling two pairs:

We can roll the map and encircle a quad:

HO: Simplify the following map.

Solution:

HO: Simplify the following map.

Solution:

Simplification Procedure for Karnaugh maps

Pair Reduction Rule : Remove the variable which changes its state from complemented to uncomplemented or vice versa.Pair removes one variable only.

Quad Reduction Rule : Remove the two variables which change their states.A quad removes two variables.

Octet Reduction Rule : Remove the three variables which changes their state.Octet removes three variables.

Map Rolling : Map rolling means roll the map considering the map as if its left edges are touching the right edges and top edges are touching bottom edges.While marking the pairs quads and octet, map must be rolled.

Overlapping Groups : Overlapping means same 1 can be encircled more than once. Overlapping always leads to simpler expressions.

Redundant Group : It is a group whose all 1's are overlapped by other groups. Redundant groups must be removed. Removal of redundant group leads to much simpler expression.

 

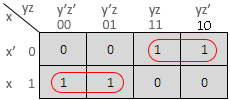
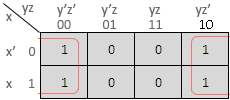
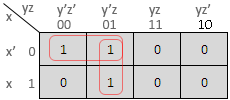
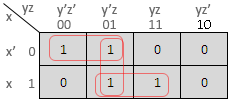
Ex. 1 : Represent the following boolean expression in a K-map and simplify.

F = x'yz + x'yz' + xy'z' + xy'z

Solution :

The K-map is as follows :

Hence the simplified expression is

F = x'y + xy'

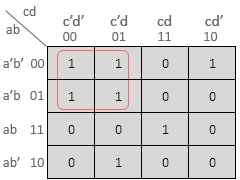
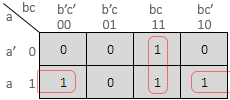
Ex. 2 :Simplify the following boolean expression using K-map.

F = a'bc + ab'c' + abc + abc'

Solution :

The K-map is as follows :

Hence the simplified expression is

F = bc + ac'